Local density of states in clean two-dimensional superconductor–normal metal–superconductor heterostructures
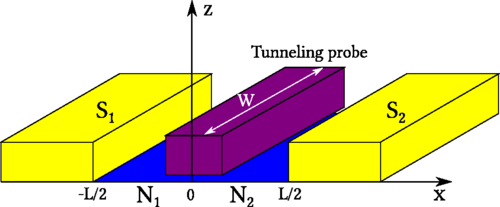
Motivated by recent advances in the fabrication of Josephson junctions in which the weak link is made of a low-dimensional nonsuperconducting material, we present here a systematic theoretical study of the local density of states (LDOS) in a clean two-dimensional normal metal (N) coupled to two s-wave superconductors (S). To be precise, we employ the quasiclassical theory of superconductivity in the clean limit, based on Eilenberger's equations, to investigate the phase-dependent LDOS as a function of factors such as the length or the width of the junction, a finite reflectivity, and a weak magnetic field. We show how the spectrum of Andreev bound states that appear inside the gap shape the phase-dependent LDOS in short and long junctions. We discuss the circumstances when a gap appears in the LDOS and when the continuum displays a significant phase dependence. The presence of a magnetic flux leads to a complex interference behavior, which is also reflected in the supercurrent-phase relation. Our results agree qualitatively with recent experiments on graphene SNS junctions. Finally, we show how the LDOS is connected to the supercurrent that can flow in these superconducting heterostructures and present an analytical relation between these two basic quantities.
D. Nikolić, W. Belzig, and J. C. Cuevas, Phys. Rev. Research 1, 033031
